Пусть ABC - произвольный треугольник (рис.1 или 2 или 3); проведем биссектрису угла C, затем ось симметрии стороны AB (т.е. прямую, перпендикулярную к AB в середине M отрезка AB) и рассмотрим различные случаи взаимного расположения этих прямых; так как в рассуждениях участвуют только одна биссектриса и одна ось симметрии, то разрешим себе их называть просто "биссектриса" и "ось".

Случай 1: биссектриса и ось не пересекаются,
т.е. либо параллельны, либо сливаются. Так как ось перпендикулярна к AB, т.е. совпадает с высотой, а в таком случае треугольник ABC - равнобедренный (CA=CB).

Случай 2: биссектриса и ось не пересекаются внутри
треугольника ABC
(рис.1), пусть в точке N. Так как эта точка равноудалена от сторон угла ACB, то, опустив из нее перпендикуляры NP и NQ соответственно на CB и CA, имеем NP=NQ. 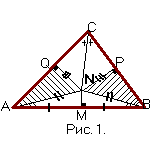Но точка N в тоже время равноудалена от концов отрезка AB, т.е. NB=NA. Прямоугольные треугольники NPB и NQA равны по катету и гипотенузе, следовательно, угол NAQ равен углу NBP. Прибавляя к этим равным углам равные между собой (как углы при основании равнобедренного треугольника  ANB)   углы  NAB  и  NBA,    получим угол CAB, равный углу CBA, значит, треугольник ABC - равнобедренный (именно CA=CB).

Случай 3: биссектриса и ось пересекаются на стороне AB,
т.е. в середине M этой стороны. Это означает, что в треугольнике ABC медиана и биссектриса, проведенные из вершины C, совпадают, а отсюда следует, что этот треугольник- равнобедренный.

Замечание.
Предостерегаем читателя от возможной ошибки. Хорошо известно, что в равнобедренном треугольнике медиана и биссектриса совпадают. Но мы ссылаемся здесь не не это, а на обратное утверждение: "если в треугольнике медиана и биссектриса , проведенные из одной вершины, совпадают, то треугольник - равнобедренный". В такой формулировке обратная теорема также верна, но доказательство ее может затруднить читателя, поэтому приводим одно из возможных. Пусть в треугольнике ABC отрезок CM - одновременно медиана и биссектриса. Опустив из точки M перпендикуляры MP и MQ на стороны CB и CA (можно воспользоваться рис. 1, считая там точки M и N совпадающими; при этом прямая MN становится лишней), получаем равные прямоугольные треугольники MPB и MQA, а затем из равенства углов MBP и MAQ заключаем, что треугольник ABC - равнобедренный. Это рассуждение будет неполным, если не показать, что точки P и Q попадут именно на стороны CB и CA, а не на их продолжения. Одна из точек могла бы попасть на продолжение соответсвующей стороны, если бы один из углов A и B был тупым. Пусть, например, угол B - тупой, так что   точка P лежит на продолжении стороны CB; по-прежнему   получается угол MAQ равен углу MBP, но теперь это приводит к противоречию, так как первый из этих углов - внутренний для треугольника ABC, а второй - внешний, с первым не смежный.

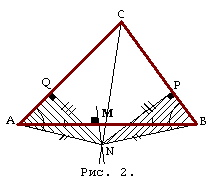
Случай 4а: биссектриса и ось пересекаются вне треугольника ABC; перпендикуляры, опущенные из точки N пересечения на стороны CB и CA, падают на эти стороны (рис. 2), а не на их продолжения.
Как и раньше, получаем равные треугольники NPB и NQA, равнобедренный треугольникANB. Углы при основании AB треугольника ABC равны теперь как разности (а не как суммы в случае 2) соответственно равных углов.

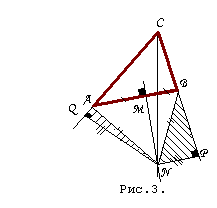
Случай 4б: биссектриса и ось пересекаются вне треугольника ABC; перпендикуляры, опущенные из точки N переечения на стороны CB и CA , падают на продолжение этих сторон (рис. 3).
Те же построения и рассуждения приводят к выводу о равенстве внешних углов при вершинах A и B треугольника ABC. Отсюда сейчас же вытекает равенство внутренних углов A и B, следовательно, CA=CB.

Анализ примера.
Рассмотрены не все возможные случаи (Здесь и дальше, говоря о возможных допущениях или о возможных случаях, мы вовсе не утверждаем, что все они действительно возможны в условиях данного примера. Наоборот, не раз случается, что допущенный нами сначала в качестве возможного случай потом окажется фиктивным, т.е. противоречащим условию или тому, что считается установленным, как это часто бывает в доказательствах "от противного". Таким образом, речь идет всегда о так называемых "априорных возможностях " (от  a priori- заранее), т.е. о возможностях, которые представляются заранее, до учета остальных условий вопроса. ), именно не учтена возможность того, что из двух перпендикуляров NP и NQ один упадет на сторону треугольника ABC, а другой - на продолжение стороны (рис. 4, где пока не надо принимать во внимание окружность). Если это произойдет, то один из углов при основании AB треугольника ABC окажется разностью двух углов, а другой будет смежным для суммы тех же углов - отсюда, разумеется, никаких выводов, относящихся к углам при основании, а значит, и к равенству боковых сторон, сделать нельзя. Достаточно установить этот пробел в доказательстве, для того чтобы оно было опорочено. Более того, если данный треугольник - неравнобедренный, то можно утверждать (рассуждая от противного), что все рассмотренные случаи (рис. 1, 2 и 3) невозможны, а единственно возможный случай (рис. 4) упущен.

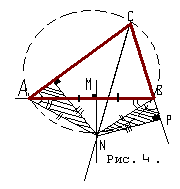
Впрочем, мы дадим сейчас прямое доказательство того, что в неравнобедренном треугольнике расположение частей фигуры именно таково, каким оно изображено на рис. 4. Действительно, пусть CA>CB. Опишем около треугольника ABC окружность; по свойству вписанных углов биссектриса угла C должна пройти через середину N дуги AB, на которую этот угол опирается. Но через ту же середину N должна пройти   ось  симметрии   хорды AB. Таким образом, пересечение биссектрисы с  осью  происходит  на   описанной   окружности,  т.е.   заведомо   вне   треугольника ABC. Перпендикуляры из N на CA и CB упадут на эти стороны или  их   продолжения  в   зависимости  от  того,   будут   ли   острыми  или  тупыми углы NAC, NBC. Вместо этих вписанных углов мы будем рассматривать  дуги,   на  которые  они опираются. Так как мы предположили CA > CB, то дуга CA больше дуги CB, а отсюда и из равенства дуг AN и BN следует, что дуга CAN больше дуги CBN. Это означает, что дуга CAN больше полуокружности, а дуга CBN меньше ее, следовательно, угол  CBN  тупой,   а  угол CAN острый. Поэтому перпендикуляр  NP  падает  на продолжение стороны CB, а перпендикуляр NQ на сторону AC (в качестве упражнения предлагаем читателю доказать, что точки P, M, Q лежат на одной прямой).